Was ist Wärme?
Einleitung
Wir wenden den weitaus größten Teil unseres Energieverbrauchs zur Erzeugung von Wärme auf. Wärme scheint etwas zu sein, dass wir gerne haben und für dessen Erzeugung wir einen hohen Preis zu zahlen bereit sind. Um Energie zu sparen ist es sicher sinnvoll, die Wärmeerzeung genauer zu analysieren, denn wo der größte Verbrauch ist, sollte auch das größte Einsparpotenzial sein. Um dies aber tun zu können, muss man wissen, was Wärme ist - eine keineswegs einfache Frage.
Die meisten Menschen werden auf die Frage die gefühlte Wärme etwa des Badewassers, so eine Art gefühlter, recht hoher Temperatur, beschreiben. Andere werden angeben, Wärme ist, wenn die Temperatur hoch ist, aber unter "Hitze" liegt. Vielleicht kann Wärme auch das Gegenteil von Kälte sein, was allerdings die Frage aufwirft, was Kälte ist.
Aus physikalischer Sicht sind alle diese Vorstellungen falsch. Wärme ist nicht das gleiche wie Temperatur und wird auch nicht in °C gemessen und "Kälte" gibt es im Prinzip gar nicht. Wärme kann also nicht das Gegenteil davon sein. Was aber ist dann Wärme?
Wärme ist Energie
Aus der Sicht des Physikers ist Wärme eine Form der Energie und sollte vielleicht treffender "Wärmeenergie" als "Wärme" genannt werden. Die Wärmeenergie wird, wie jede andere Energieform auch, in Joule (J) oder Kilowattstunden (kWh) gemessen (vgl. dazu auch: "Was ist Energie?").
Die Temperatur ist lediglich ein "Maß" für die Wärme - wenn ein Körper eine höhere Temperatur annehmen soll, dann muss ihm Energie, genauer Wärmeenergie, zugefügt werden. Nimmt der Körper diese Energie auf, steigt seine Temperatur; und zwar umso stärker, je mehr Energie hinzugefügt wurde. Die Energie wird dann als Teilchenbewegung in dem Körper gespeichert. Diese Teilchenbewegung ist es, die von uns als "Wärme" wahrgenommen oder empfunden wird. Im Folgenden werden diese Zusammenhänge etwas detaillierter beschrieben.
Temperatur
Zur Messung der Temperatur, einem Maß für die Wärme, wurden im Laufe der Zeit etliche unterschiedliche Einheiten definiert, von denen aber heute nur noch wenige gebräuchlich sind. In Deutschland ist die Angabe in °C (Grad Celsius) üblich und in den Naturwissenschaften sollte man K (Kelvin) verwenden. Einen Überblick über weitere Einheiten liefert der Wikipediaartikel zur Temperatur, der auch viele weitere Information zur Temperatur bietet.
Celsiusskala

Die Celsiusskala geht auf Anders Celsius zurück, nach dem die Einheit °C auch benannt wurde. Grundlage der Celsiusskala bildet das Wasser. Der Nullpunkt der Celsiusskala ist der Schmelzpunkt von Wasser bei Normaldruck. Mehr oder weniger willkürlich erfolgte dann die Festlegung, dass der Siedepunkt von Wasser bei Normaldruck 100 °C ist; der Bereich zwischen Schmelz- und Siedetemperatur des Wassers bei Normaldruck ist also in hundert Abschnitte eingeteilt, von denen jeder einer Temperaturdifferenz von 1°C entspricht.
Die Celsiusskala ist im Alltag sehr praktisch, da sie für die üblichen Temperaturen unseres Lebens kleine Zahlenwerte liefert. Außerdem lässt sich am Vorzeichen leicht eine eventuelle Glättegefahr ablesen, d.h. Frost lässt sich an negativen Werten für die Temperatur erkennen.
Aus physikalischer Sicht ist die Cesiusskala aber höchst unpraktisch, da sich an einer "willkürlichen" Stelle plötzlich das Vorzeichen der Temperatur ändert. Außerdem bedeutet eine Temperatur von 0°C nicht, dass in dem Körper keine Energie gespeichert ist. Auch verdoppelt sich die im Körper gespeicherte Energie nicht, wenn sich die Temperatur in °C verdoppelt. Dies ist höchst unpraktisch, wenn man Wärmeenergie genauer betrachten möchte.
Kelvinskala

Die Kelvinskala löst alle Probleme der Celsiusskala. Eine Temperatur von 0 K liegt dann vor, wenn die Bewegungsenergie aller Teilchen eines Körpers und somit auch die im Körper gespeicherte Wörmeenergie 0 wird. Damit gibt es keine negativen Temperaturen, denn weniger als keine Wärmeenergie kann ein Körper nicht enthalten und ein Abkühlen unter 0 K ist demzufolge nicht möglich. Die Intervallbreite der Kelvinskala stimmt mit der der Celsiusskala überein, d.h. erwärmt man einen Körper um 1 K erwärmt man ihn auch um 1 °C und zwischen dem Schmelz- und dem Siedepunkt von Wasser liegen genau 100 K. Der Nullpunkt der Kelvinskala liegt bei etwa -273,13 °C. Wasser schmilzt demnach bei 273,13 K bzw. 0°C und es siedet bei 373,13 K bzw. 100 °C.
Aus physikalischer Sicht hat die Kelvinskala den Vorteil, dass die Wärmeenergie eines Körpers tatscählich proportional zur Temperatur in Kelvin ist - d.h. bei doppelter Temperatur in Kelvin verdoppelt sich auch die Wärmeenergie.
Makroskopische Betrachtung
Makroskopische Betrachtung bedeutet, dass wir einen großen Körper als ganzes betrachten und versuchen, die Wärmeenergie zu bestimmen, ohne dass wir uns dafür interessieren, wie die Wärmeenergie im Detail in der Teilchenbewegung gespeichert ist.
Misst man die Energiemenge, die nötig ist, um z.B. einen Liter Wasser um 1°C zu erwärmen, stellt man fest, dass diese Menge immer gleich ist, egal ob man dass Wasser von 1°C auf 2°C erwärmt oder von 98°C auf 99°C. Erst, wenn man den Siedepunkt überschreitet oder den Schmelzpunkt unterschreitet, d.h. den Aggregatzustand ändert, ändert sich die jeweils erforderliche Energiemenge. Außerdem stellt man fest, dass zum Schmelzen oder zum Sieden Energie erforderlich ist. Am Beispiel des Wassers, wird dieser Sachverhalt im Folgenden etwas genauer betrachtet.
Temperaturkurve von Wasser
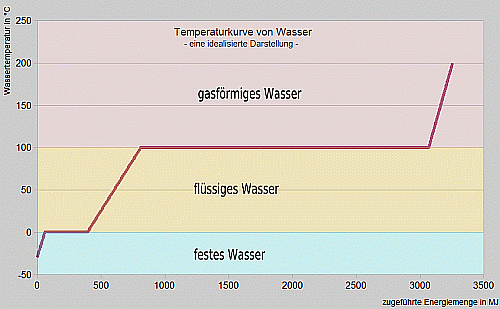
Die Temperaturkurve wurde mit Zahlenwerten von Wikipedia vom 15.06.2009 berechnet. Dass die Wärmekapazität temperaturabhängig ist, wurde hierbei vernachlässigt. In unserem Modellexperiment nehmen wir 1 kg Wasser, also etwa 1 Liter, und kühlen das Wasser auf -30 °C ab. Nun fügen wir dem Wasser eine bekannte Menge Energie hinzu und messen die Temperatur des Wassers, bis diese 200°C erreicht. Wir starten also mit einem Eisblock, erhalten zunächst flüssiges und später gasförmiges Wasser und messen die Temperatur in Abhängigkeit von der zugeführten Energiemenge.
Die so erhaltene Temperaturkurve ist in der Abbildung dargestellt. Man sieht, dass die Temperatur zunächst mit der zugeführten Energiemenge linear ansteigt - die zugeführte Energie wird also zum Erwärmen des Eises genutzt. Zum Erwärmen eines 1 kg Eises um 1 °C benötigt man ca. 2060 J Energie. Dieser Wert lässt sich mathematisch aus der Steigung der Geraden unterhalb 0°C erhalten.
Wenn die Temperatur 0°C erreicht, steigt sie zunächst trotz weiterer Energiezufuhr nicht mehr an. Die zugeführte Energie kann also die Temperatur nicht weiter erhöhen, sondern wird dafür verwendet, das Eis zu Schmelzen - um 1 kg 0°C kaltes Eis in 1 kg 0°C kaltes Wasser zu verwandeln, sind 332,5 kJ = 332500 J Energie nötig. So lange nun noch festes Wasser vorhanden ist, wird die zugeführte Energie näherungsweise vollständig zum Schmelzen des Eises verwendet. Die Energie, die zum Schmelzen eines Stoffes ohne Temperaturänderung nötig ist, wird Schmelzwärme genannt. Sie beträgt für Wasser 332,5 kJ/kg.
Wenn das Wasser vollständig geschmolzen ist, wird die zugeführte Energie wieder vollständig zum Erwärmen des Wassers verwendet und die Temperatur steigt wieder linear mit der zugeführten Energie an, allerdings ist die Kurve flacher. Es ist also mehr Energie nötig, um 1 kg flüssiges Wasser um 1 °C zu erwärmen, als für 1 kg festes Wasser - genau sind pro kg Wasser für jedes Grad mehr 4187 J Energie nötig.
Wenn die Temperatur 100°C erreicht, steigt sie trotz weiterer Energiezufuhr nicht mehr weiter an, weil erneut Energie zum ändern des Aggregatzustandes, diesmal von flüssig nach gasförmig, aufgewendet werden muss; die sogenannte Verdampfungswärme. Für Wasser beträgt sie etwa 2257000 J/kg. Um also 1kg Wasser bei 100°C ohne Temperaturerhöhung zu verdampfen, sind 2257000J = 2257 kJ = 2,257 MJ Energie nötig.
Erst wenn alles Wasser gasförmig ist, führt eine weitere Energiezufuhr auch wieder zu einer Temperaturerhöhung des nun gasförmigen Wassers. Um nun die Temperatur des 1kg Wasserdampfes um 1°C zu erhöhen, sind etwa 1870 J Energie nötig - der Kurvenverlauf ist also steiler als im flüssigen Bereich, denn für die gleiche Temperaturerhöhung ist eine kleinere Energiemenge nötig.
Die spezifische Wärmekapazität
| Stoff | Wärmekapazität |
|---|---|
| Wasser | 4186 J/(kg·°C) |
| Ethanol | 2,42 J/(kg·°C) |
| Aluminium | 0,90 J/(kg·°C) |
| Beton | 0,92 J/(kg·°C) |
| Fensterglas | 0,17 J/(kg·°C) |
| Eichenholz | 2,39 J/(kg·°C) |
| Stahl | 0,47 J/(kg·°C) |
| Mauerwerk | 0,86 J/(kg·°C) |
Wie im Diagramm bereits zu sehen ist, steigt die Temperatur linear mit der zugeführten Energiemenge an - zum Erwärmen eines Körpers um die immer gleiche Temperaturdifferenz ist also immer die gleiche Energiemenge erforderlich, sofern keine Änderung des Aggregatszustandes erfolgt. Die Energiemenge, die nötig ist, um eine bestimmte Menge eines Stoffes um 1°C zu erwärmen, wird spezifische Wärmekapazität genannt. Sie wird oft in der Einheit J/(kg·°C) angegeben. Tatsächlich ist die Wärmekapazität nur ungefähr konstant und ändert sich mit der Temperatur etwas. Im Folgenden vernachlässige ich diesen Effekt jedoch. Hierdurch wird die spezifische Wärmekapazität zu einer Eigenschaft des Stoffes, die für den Stoff, etwa Wasser oder Aluminum oder Eisen oder... charakteristisch und immer gleich ist. Einige Beispiele für spezifische Wärmekapazitäten sind in der Tabelle angegeben. Alle Werte stammen aus "Das große Tafelwerk interaktiv, Formelsammlung für die Sekundarstufen I und II", Cornelsen Verlag Berlin, 2003, S. 101.
Natürlich sind die Werte für Eichenholz, Beton, Mauerwerk, Stahl und Fensterglas keine völlig exakten Werte, da es sich bei diesen "Stoffen" um Mischungen handelt, deren Wärmekapazität vom Mischungsverhätnis abhängig ist. Allerdings sollten die konkreten Werte nicht allzu weit von denen in der Tabelle abweichen, sodass die Tabelle hier zumindest einen Richtwert bieten kann.
Energiemenge berechnen
Kennt man die Wärmekapazität eines Stoffes oder Körpers, so lässt sich die Energie ausrechnen, die insgesamt in ihm gespeichert ist, aber auch die Energie, die nötig ist, um eine bestimmte Temperatur zu erreichen. So ließe sich beispielsweise die Energiemenge berechnen, die zum Duschen mindestens nötig ist, weil sie zum Erwärmen des Wassers benötigt wird. Blickt man in ein Physikbuch, so findet man eine Formel der folgenden Art:
ΔQ=m·C·ΔT
ΔQ: erforderliche Wrmemenge in J
m: Masse des Stoffes oder Krpers in kg
C: Spezische Wrmekapazität in J/(°C·kg)
ΔT: Temperaurdifferenz in °C
Was der Physiker hier in eine für den Laien kompliziert erscheinende Formel presst, ist im Grunde ganz einfach. Da die spezifische Wärmekapazität angibt, wieviel Energie erforderlich ist, um 1kg eines Stoffes um 1°C zu erwärmen, muss man einfach "nur" die Anzahl der Kilogramms mit der gewünschten Temperaturänderung und der Wärmekapazität multplizieren. Zur besseren Veranschaulichung betrachten wir ein paar Beispiele:
Beispiel 1: Energiebedarf beim Duschen
Zum Duschen muss kaltes Wasser auf eine angenehme Temperatur erwrämt werden. Nehmen wir an, das "kalte" Wasser hätte eine Temperatur von 10°C und es soll bei 32°C geduscht werden, so ergäbe sich ein ΔT von 32°C-10°C=22°C. Wenn wir zum Duschen etwa 40 Liter Wasser, also etwa 40kg Wasser benötigen, so ergibt sich mit der Wärmekapazität aus der obigen Tabelle:
gegeben: C=4186J/(°C·kg), ΔT=22°C, m=40kg
gesucht: ΔQ
ΔQ = 40kg · 4186J/(°C·kg) ·
22°C = 3683680 J ≈ 3,68 MJ ≈ 1kWh ≈ 880 kcal
Um also wie oben angegeben zu Duschen, sind alleine zum Erwärmen des Wassers 3,7 Mio Joule oder etwa 1 kWh oder 880 kcal Energie nötig. Nebenbei bemerkt: Die meisten Leute werden wärmer und mit mehr Wasser duschen.
Beispiel 2: Energieverbrauch beim Eisessen
Mein Diätplan: Ich lutsche Eiswrfel und nehme ab, weil ich das Eis schmelzen und dann das Wasser von 0°C auf 37°C erwärmen muss. Hierzu ist Energie erforderlich und ich verbrenne mehr Kalorien, Ähnlich wie beim Sport. Wie viele Eiswürfel zu je 20g sind erforderlich, um 1 kg Körperfett abzubauen? Aus verschiedenen Internetquellen geht hervor, dass 1kg Körperfett etwa 7000 kcal sind.
Die Lösung ist etwas komplizierter als in Beispiel 1. Zunächst sollte man die kcal in J umrechnen:
7000 kcal · 4,186 kJ/kcal = 29302 kJ ≈ 29,3 MJ
Pro Kilogramm Körperfett müsste ich also insgesamt etwa 29,3 MJ Energie für das Schmelzen und Erwärmen aufwenden.
Die Schmelzwärme von Eis beträgt etwa 332,5 kJ/kg, d.h. zum Schmelzen von 1kg Eis sind 332,5kJ Energie nötig. Um das hierdurch entstehende 1kg Wasser dann auf 37° zu erwärmen ist die folgende Energie nötig:
ΔQ = 1 kg · 4186J/(°C·kg) · 37 °C = 154882 J ≈ 154,9 kJ
Um 1kg Eis von 0°C zunächst zu schmelzen und das dabei entstehende 0°C kalte Wasser dann auf 37°C zu erwärmen sind also
332,5 kJ + 154,9 kJ = 487,4 kJ
Energie nötig. Um 1kg Körperfett umzusetzen, müsste ich aber 29,3 MJ Energie aufwenden. Es ergibt sich also eine erforderliche Eismenge von:
29302 kJ : 487,4 kJ/kg Eis = 60,1 kg Eis
Um 1kg Körperfett abzubauen müsste man also 60,1 kg Eiswrfel lutschen. Wenn einer 20g wiegt, entspricht das 50 Eiswürfeln je Kilogramm Eis also insgesamt etwa 3006 Eiswürfeln. Das Lutschen von Eiswürfeln ist also als Diät eher ungeeignet.
Mikroskopische Betrachtung
Wie bereits gesagt "ist" Wärme im Grunde nichts anderes als Teilchenbewegung. Man könnte also Wärmeenergie als Bewegungsenergie der Atome oder Moleküle betrachten und also eine Art mittlerer Bewegungsenergie pro Atom oder Molekül angeben. Dies ist mit "mikroskopischer Betrachtung" gemeint. Bei den makroskopischen Betrachtungen haben wir die spezifische Wärmekapazität, d.h. die Wärmekapazität bezogen auf 1 kg eines Stoffes betrachtet. Für eine mikroskopische Betrachtung wäre ein Bezug auf auf eine immer gleiche Teilchenzahl, 1 mol, praktischer, sodass man statt der spezifischen die sogenannte molare Wärmekapazität betrachtet.
Die molare Wärmekapazität gibt an, wie viel Energie erforderlich ist, um 1 mol eines Stoffes um 1 K (1 Kelvin) zu erwärmen. Sie wird in der Einheit J/(mol·K) angegeben und lässt sich bei bekannter molarer Masse aus der spazifischen Wärmekapazität berechnen.
Im Prinzip ist es durch die Betrachtung der Wärme als Teilchenbewegung möglich mit Mitteln der statistischen Thermodynamik alle thermodynamischen Größen aus der Struktur der Materie einigermaßen genau vorher zu sagen. Da dies aber recht kompliziert ist und mein Ziel nicht das Schreiben eines Aufsatzes zur statistischen Thermodynamik ist und der Nutzen für "Ottonormalverbraucher" auch eher klein wäre, werde ich das hier nicht vertiefen - ob ich es könnte, sei mal dahin gestellt :-)
Rätselhaftes rund um die Wärme
Gefühlte Temperaturen
Manchmal hört man im Wetterbericht von einer "gefühlten Temperatur", die teilweise einige Grad von der tatschlichen Temperatur abweicht. Auch fühlt sich 20°C kaltes Wasser deutlich kälter an, als 20°C warme Luft. Der Grund hierfür liegt in unserem Temperaturempfinden. Zum Einen empfinden wir "Wärme" sehr subjektiv. Probiere es aus: Stelle vier Schüsseln Wasser vor Dich, von denen die Linke sehr kaltes und die Rechte sehr heißes Wasser enthält, während die beiden Mittleren gleich warmes Wasser mittlerer Temperatur enthalten. Lege nun Deine linke Hand in die Linke Schüssel und die Rechte in die Rechte Schüssel und lasse die Hände einige Zeit im Wasser. Nehme nun beide Hände gleichzeitig aus den Schüsseln und tauche sie in die beiden mittleren Schüsseln ein. Obwohl beide Schüsseln gleich warmes Wasser enthalten, wird Dir das Wasser an Deiner linken Hand deutlich wärmer vorkommen als das an der rechten Hand. Der Grund dafür ist, dass wir Wärme unter anderem auch im Vergleich zur vorherigen Situation empfinden.
Zum Anderen nehmen wir niemals eine Temperatur wahr, sondern eher einen Verlust bzw. eine Aufnahme von Wärmeenergie. Wenn ein Gegenstand unserem Körper viel Wärmeenergie entzieht, fühlt er sich sehr kalt an. Fügt der Gegenstand unserem Körper viel Wärmeenergie hinzu, fühlt er sich sehr warm/heiß an.
Warum fühlen sich Metalle kalt an?
Nimmt man einen Metall- und einen Holzlffel aus der Schublade, so fühlt sich der Holzlöffel viel wärmer an, obwohl beide schon lange in der Schublade lagen und sicher die gleiche Temperatur wie die Luft im Raum besitzen, also gleich warm sind. Der Grund für das unterschiedliche Temperaturempfinden ist die unterschiedliche Wärmeleitfhigkeit. Metall ist ein sehr guter Wärmeleiter, d.h. Wärmeenergie wird in Metallen schnell geleitet, weil sich die erhöhte Bewegungsenergie einzelner Atome schnell auf das gesamte Metall verteilen kann. Holz ist ein eher schlechter Wärmeleiter, wodurch sich die erhöhte Bewegungsenergie einzelner Atome nicht so schnell verteilen kann.
Nimmt man also einen Holzlöffel in die Hand, so erwärmt man näherungsweise nur den Teil des Holzes, den man direkt berührt. Der Rest des Löffels behält seine vorherige Temperatur. Es fließt also nur eine kleine Menge Wärmeenergie aus dem Körper in den Löffel, weil nur ein kleiner Teil des Löffels erwärmt wird.
Nimmt man nun einen Löffel aus Metall in die Hand, so fließt die Wärme schnell von der Berührungsstelle in den Rest des Löffels ab. Man erwärmt also den gesamten Löffel und nicht nur die Berührungsstelle. Es fließt also mehr Wärmeenergie aus dem Körper in den Löffel, wodurch sich der Löffel kälter anfühlt.
Warum fühlt sich Luft auf nasser Haut kälter an als auf trockener?
Jeder kennt das: Man ist im Sommer schwimmen. Bevor man ins Wasser geht kommt einem die Luft unerträglich heiß vor. Kommt man dann aus dem Wasser erscheint einem die Luft viel kühler. Wie kommt das?
Natürlich sorgt das unter Umständen kalte Wasser für einen Teil der Abkühlung. Die paar kleinen Tropfen, die sich auf dem Körper befinden, sollten sich aber in der Sonne schnell erwärmen und also nicht mehr "kühl" sein. Trotzdem fühlt es sich kühler an und der Grund dafür ist nur zu einem kleinen Teil die "Kühle" des Wassers. Der Hauptgrund ist der Trocknungsprozess. Während man trocknet verdampft das Wasser, es ändert also seinen Aggregatzustand. Hierzu ist Energie erforderlich, die zu einem erheblichen Teil dem Körper entzogen wird. Die Verdampfungswärme (s.o.) des Wassers führt also dazu, dass unserem Körper Wärmeenergie entzogen wird. Diesen Verlust an Wärmeenergie empfinden wir aber als "Kälte", also fühlt sich die Luft kühler an.
Warum ist Wasser "kälter" als gleich warme Luft?
Niemand käme auf die Idee mit 20°C kaltem Wasser "warm" zu duschen, als Wohnzimmertemperatur ist es aber ganz angenehm. Komisch. Die Erklärung ist auch hier wieder die dem Körper entzogene Energiemenge.
Da unsere Körpertemperatur mit 37°C deutlich über den 20°C liegt, erwärmt unser Körper die umgebende Luft bzw. das umgebende Wasser. Da nun Luft eine ziemlich geringe Dichte hat, haben wir an unserer Körperoberflche nur mit einer relativen kleinen Menge Luft Kontakt und können also auch nur diese relativ kleine Menge Luft erwärmen. Wasser hat eine viel größere Dichte und wir haben folglich mit viel mehr Wasser kontakt und erwärmen also viel mehr Wasser. Hinzu kommt, dass Wasser eine deutlich höhere Wärmekapazität als Luft hat.
Zum Erwärmen der unseren Körper umgebenden Luftschicht ist also nur eine kleine Menge Energie nötig - zum Erwärmen einer Wasserschicht hingegen eine sehr viel größere Menge Energie. Da diese Energie in beiden Fällen unserem Körper entzogen wird, empfinden wir den kleinen Energieabfluss an Luft als nicht so schlimm, haben aber bei dem großen Energieabfluss in Wasser ein deutliches Kälteempfinden, obwohl die Temperaturen gleich sind.
Warum fühlt sich "Wind" kühler an als Windstille?
Wie bereits beschrieben, erwärmt unser Körper die uns umgebende Luft, wozu Wärmeenergie aus dem Körper in die Luft wechselt. Die Luftschicht mit Kontakt zu unser Haut wird dadurch also erwärmt, was zur Folge hat, dass weniger Wärme aus unserem Körper in diese stetig wärmer werdende Luftschicht fließt, da sich die Lufttemperatur der Körpertemperatur immer weiter annähert. Wird nun durch den Wind die Luftschicht mit Kontakt zur Haut ständig ausgewechselt, kommt es nie zu einer Temperaturannäherung und die Luft mit Kontakt zur Haut ist stetig kühl, wodurch dem Körper mehr Wärme entzogen wird und wir trotz gleicher Lufttemperatur eine niedrigere Temperatur "fühlen".
Warum schwitzen wir?
Unser Körper setzt pausenlos Energie um, und zwar umso mehr, je mehr wir uns anstrengen. Hierbei ist er aber nicht besonders effizzient, sondern wandelt den größten Teil der Energie in Wärme um. Bei körperlicher Anstrengung wird also in unseren Muskeln eine große Menge Wärmeenergie freigesetzt. Hierdurch würde jetzt eigentlich unsere Körpertemperatur steigen, was jedoch nicht geschehen darf. Also muss diese "Abwärme" unserer Muskeltätigekeit möglichst schnell aus dem Körper geschafft werden. Zu diesem Zweck überzieht sich der Körper punktuell oder überall, je nach Wärmemenge, mit einer Wasserschicht, die dem Körper dann beim Verdunsten Wärme entzieht, wie bereits in "Warum fühlt sich Luft auf nasser Haut kälter an als auf trockener?" beschrieben. Schwitzen ist also unsere körpereigene Klimaanlage, die dafür sorgt, dass unsere Körpertemperatur bei körperlicher Anstrengung oder hoher Lufttemperatur nicht übermig ansteigt.
