Die Geschwindigkeit chemischer Reaktionen

Geschwindigkeit - wir alle kennen den Begriff. Eine höhere Geschwindigkeit bedeutet, dass wir uns schneller bewegen. Eigentlich ganz einfach. Eine höhere Reaktionsgeschwindigkeit heißt also, dass eine chemische Reaktion schneller ist. Kurz nachgedacht: Die "Reaktion" bewegt sich aber nicht. Was heißt also genau "schneller" in diesem Zusammenhang? Kann man das auch mit einer Art "Tacho" messen und was genau misst der dann? Und zuletzt - beim chemischen Gleichgewicht klang es ja schon an - man kann die Reaktionsgeschwindigkeit beeinflussen. Aber wie und warum geht das?

Definition der Reaktionsgeschwindigkeit

Da die Reaktionsgeschwindigkeit eine "Geschwindigkeit" ist, sollte die Definition so ähnlich sein, wie bei der Geschwindigkeit von Bewegungen. Also gucken wir uns die zunächst etwas genauer an und kommen dann zur Geschwindigkeit chemischer Reaktionen.

Exkurs: Geschwindigkeit bei Bewegungen

Nehmen wir an, ein Auto legt in einer Stunde eine Strecke von 100 km zurück. In diesem Fall könnte vermutlich jeder die "Durchschnittsgeschwindigkeit" ausrechnen. Das Auto ist 100 km/h gefahren. Um die Geschwindigkeit auszurechnen, teilen wir also den zurück gelegten Weg durch die Zeit.

Geschwindigkeit = Weg durch Zeit
v = s / t

Sehr einfach aber leider nicht so richtig gut, denn das Auto ist bestimmt nicht die ganze Stunde immer genau 100 km/h schnell gewesen. Der Fahrer ist sicher mal schneller und mal langsamer gefahren. Nur im Durchschnitt über die gesamte Zeit lag die Geschwindigkeit bei 100 km/h. Wie bekommen wir nun die Geschwindigkeit in jedem Augenblick? Betrachten wir dazu zunächst das Weg-Zeit-Diagramm solcher Bewegungen.

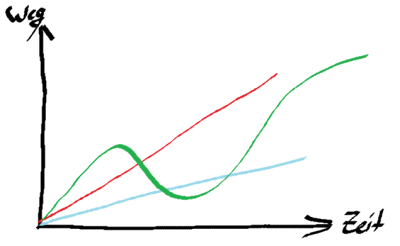
Beschränken wir uns zunächst auf die blaue und die rote Linie und lassen die grüne außer acht. Welche Bewegung ist schneller? Die Rote, denn in der gleichen Zeit wird eine größere Strecke zurück gelegt. Die rote Linie verläuft steiler als die blaue und deshalb muss die Geschwindigkeit größer sein.

Übertragen wir das auf die grüne Linie: Sie verläuft zunächst sehr steil, denn flacht sie ab und fällt sogar wieder ab. Am Anfang ist die Geschwindigkeit also relativ hoch und fällt dann am Hochpunkt der Kurve auf null ab, denn hier vergeht Zeit, ohne dass Weg zurück gelegt wird. Danach wird die zurück gelegte Strecke wieder kleiner. Die Bewegung verläuft also wieder zum Ausgangspunkt zurück, was physikalisch eine negative Geschwindigkeit wäre. Die Geschwindigkeit lässt sich also an der Steilheit der Kurve, mathematisch der Steigung, im Zeit-Weg-Diagramm ablesen.

Die Geschwindigkeit ist die Steigung des Grafen im Zeit-Weg-Diagramm

Fehlt noch die mathematische Lösung: Wir müssten die Steigung der grünen Kurve an jedem beliebigen Punkt bestimmen können. Mit der obigen Formel v=s/t bestimmen wir die "durchschnittliche" Geschwindigkeit, also auch die durchschnittliche Steigung. Um die Momentangeschwindigkeit, also die Steigung an einem beliebigen Punkt bestimmen zu können, müssten wir eine kürzere Zeitspanne als eine Stunde betrachten; idealerweise nur einen Augenblick. Wir betrachten also ein seeeehr kurzes Zeitintervall Δt und das in dieser Zeit zurück gelegte Wegintervall Δs. Dann erhalten wir die Durchschnittsgeschwindigkeit in diesem Intervall mit v = Δs / Δt. Immer noch haben wir eine Durchschnittsgeschwindigkeit aber in einem kleineren Intervall und sind somit viel näher an der Momentangeschwindigkeit. Je kleiner wir jetzt das Zeitintervall machen, desto näher kommen wir der Momentangeschwindgkeit. Ideal wäre eine breite von Null, was aber mathematisch (Division durch 0) nicht geht - also nähern wir uns so nah wie möglich an 0 an. Wir lassen Δt gegen 0 gehen. Dann wird aus dem Δ formal-mathematisch ein "d" und wir bekommen die Momentangeschwindigkeit als Steigung im Punkt an der Stelle mit v = ds/dt, was mathematisch der "Ableitung" der Funktion für die Strecke s entspricht.

v = Δs / Δt bzw. v = ds(t) / dt = s'(t)

Die Geschwindigkeit ist die erste Ableitung des Weges nach der Zeit.

Übertragung auf die Reaktionsgeschwindigkeit

Die Reaktionsgeschwindigkeit gibt also die zeitliche Änderung irgendeiner Größe in unserer chemischen Reaktion an. Aber welche? Betrachten wir als Beispiel die Reaktion von Zink mit einer Säure:

2 H⁺ + Zn → H₂ + Zn²⁺

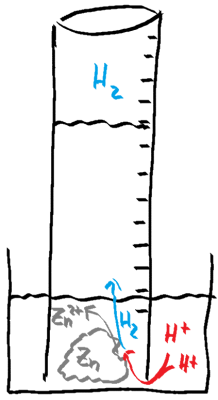
Diese Reaktion bietet durch das gasförmig entweichende Reaktionsprodukt Wasserstoff eine Reihe von Vorteilen für die Untersuchung der Reaktionsgeschwindigkeit:

• Der gasförmige Wasserstoff lässt sich leicht auffangen. Die Messung des Wasserstoffvolumens erlaubt es, den Ablauf der Reaktion quantitativ zu erfassen.
• Der gasförmige Wasserstoff verlässt den Ort der Reaktion und steht somit für eine Rückreaktion nicht zur Verfügung. Die Reaktion ist also näherungsweise keine Gleichgewichtsreaktion und es entfällt eine große Schwierigkeit: Bei Gleichgewichtsreaktionen sind alle Veränderungen des Reaktionsgemisches immer eine Folge von Hin- und Rückreaktion. Durch das Unterdrücken der Rückreaktion beobachten wir tatsächlich nur eine Reaktion.

Das Analogon des Weges: Konzentration

Der erste Gedanke ist: Wir messen das Volumen des Wasserstoffs und nehmen die Volumenänderung als Reaktionsgeschwindigkeit. Allerdings ist diese Idee eher schlecht, denn bei den meisten Reaktionen entsteht ja kein Gas und die Definition der Reaktionsgeschwindigkeit soll allgemeine Gültigkeit haben.

Der zweite, nur wenig bessere Gedanke wäre, die Teilchenzahl des Wasserstoffs als Basis zu nehmen und die Reaktionsgeschwindigkeit über die Zahl der in jedem Augenblick neu gebildeten Produktmoleküle zu definieren. Klingt super, ist es aber nicht, denn auch hier fehlt die Allgemeingültigkeit. Wenn ich die gleiche Reaktion nämlich erneut mache aber von allem doppelt so viel nehme, wäre sie doppelt so schnell, obwohl eigentlich alles gleich ist. Mit der Teilchenzahl als Basis würde die Reaktionsgeschwidigkeit davon abhängen, wie groß das Gefäß ist. Das wäre so ähnlich wie die Geschwindigkeit eines Autos über Zahl der Sitzplätze zu definieren. Je mehr Sitze desto schneller - eher doof.

Der dritte, jetzt wirklich gute Gedanke: Wir betrachten die Änderung der Teilchenzahl in einem bestimmten Volumen, etwa einem Liter. Wir rechnen also immer aus, wie es wäre, wenn wir genau einen Liter Volumen hätten. Das ist schlau, denn dann können wir das Gefäß so groß oder klein machen, wie wir wollen - wir betrachten ja immer den hypothetischen Liter. Wir beziehen also das Volumen in unsere Messgröße mit ein und berechnen die Zahl der Moleküle pro Liter; wir bestimmen die Konzentration c.

Reaktionsgeschwindigkeit als Konzentrationsänderung pro Zeit

Wir definieren also die Reaktionsgeschwindigkeit als Änderungsrate der Konzentration oder als Konzentrationsänderung pro Zeiteinheit. In Analogie zur Geschwindigkeit einer Bewegung erhält man dann:

v = Δc / Δt bzw. v = dc(t) / dt = c'(t)

Probleme....

Bei der Übertragung auf die obige Beispielreaktion 2 H⁺ + Zn → H₂ + Zn²⁺ treten jetzt allerdings mehrere Probleme auf:

• Das Volumen des Wasserstoffs wächst mit der Stoffmenge an. Wenn man jetzt immer den hypothetischen einen Liter betrachtet, ändert sich die Konzentration des Wasserstoffs nicht und die Geschwindigkeit der Reaktion wäre demnach mathematisch 0, obwohl die ganze Zeit weiterer Wasserstoff entsteht und demnach ganz offensichtlich eine Reaktion stattfindet.
• Das Zinkstück wird in dem Maße kleiner, wie die Zahl der Zinkatome in ihm abnimmt. Auch die Konzentration des Zinks im Zinkstück ändert sich nicht und auch hier wäre die Reaktionsgeschwindigkeit mathematisch 0.
• Die Konzentration der Protonen in der Lösung nimmt stetig ab. Ihre Konzentrationsänderung wäre demnach negativ und die Reaktionsgeschwindigkeit wäre kleiner als 0.
• Die Konzentration der Zinkionen in der Lösung wird ständig größer und die Konzentrationsänderung wäre demnach positiv und die Reaktionsgeschwindigkeit wäre größer als 0.
• Laut der Reaktionsgleichung 2 H⁺ + Zn → H₂ + Zn²⁺ ändert sich die Zahl der Protonen (H⁺) doppelt so stark wie die Zahl der Zinkionen (Zn²⁺). Der Betrag der Reaktionsgeschwindigkeit basierend auf der Protonenkonzentration wäre also doppelt so hoch, wie der Betrag basierend auf der Zinkionenkonzentration.

Je nach dem, welche Reaktionskomponente man für die Bestimmung der Reaktionsgeschwindigkeit benutzt, bekommt man also ein anderes Ergebnis. Das geht so natürlich nicht.

...und Lösungen

Wir werden bei diesem Ausweg ein paar Vereinfachung vornehmen, sodass die Lösung am Ende nicht perfekt ist aber immerhin das obige Beispiel gut beschreibt - für andere Reaktion wären aber noch weitere Optimierungen nötig. Guck ggf. in ein Buch zur physikalischen Chemie, wenn Du es wirklich perfekt machen willst.

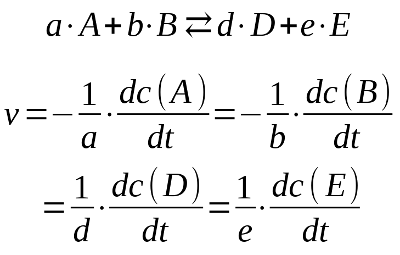
Übertragen wir diese allgemeine Definition der Reaktionsgeschwindigkeit aus der Abbildung auf unser Beispiel der Reaktion zwischen Zink und einer Säure, treffen wir folgende Vereinbarungen:

1. Wir betrachten die Reaktion in der Lösung. Da weder das feste Zink noch der gasförmige Wasserstoff gelöst sind, sind sie somit für die Definition der Reaktionsgeschwindigkeit ungeeignet. Wir benutzen den Wasserstoff um die Reaktion zu beobachten und die umgesetzte Stoffmenge zu bestimmen, definieren aber die Reaktionsgeschwindigkeit über die aus der Stoffmenge des Wasserstoffs bestimmbare Konzentrationsänderung der gelösten Ionen (H⁺ und Zn²⁺)
2. Der stöchiometrische Faktor (die Zahl vor dem Elementsymbol) fließt mit in die Definition der Reaktionsgeschwindigkeit ein. Bei den Zinkionen wäre er 1. Es ergibt sich:

v = dc(Zn²⁺) / dt

3. Wenn wir die H⁺-Ionen als Basis für unsere Reaktionsgeschwindigkeit benutzen wollen, muss das gleiche Ergebnis heraus kommen. Da sich die Protonenkonzentration doppelt so schnell verringert wie die Zinkionenkonzentration zunimmt, muss die Reaktionsgeschwindigkeit dann wie folgt definiert werden (beachte das "-½"!):

v=-½ · dc(H⁺) / dt

Insgesamt ergibt sich also für die Definition der Reaktionsgeschwindigkeit folgendes:

2 H⁺ + Zn → H₂ + Zn²⁺
v = dc(Zn²⁺) / dt = -½ · dc(H⁺) / dt

Beeinflussung der Reaktionsgeschwindigkeit

Jeder kennt den Effekt, wenn man beim Grillen in die Glut pustet: Die Glut wird intensiver und das heißt die Kohle verbrennt schneller. Das Pusten in die Glut beschleunigt also die Verbrennungsreaktion. Im Folgenden werden wir uns im Detail ansehen, welche Effekte die Reaktionsgeschwindigkeit beeinflussen. In Frage kommen folgende Faktoren:

• Zusammensetzung des Reaktionsgemisches, d.h Konzentration der an der Reaktion beteiligten Komponenten
• Temperatur
• Oberflächenbeschaffenheit und -größe bei Reaktionen an Grenzflächen
• Druck bei Reaktionen mit gasförmigen Stoffen
• Reaktionsenthalpie und Aktivierungsenergie, wobei zumindest Erstere nicht beeinflussbar ist

Beeinflussung durch Koonzentrationsänderung

Das obige Beispiel vom Grillen ist erschreckend kompliziert, denn duch das Pusten ändern sich beinahe alle der gerade aufgezählten Punkte. Den größten Effekt dürfte aber die beschleunigte Zufuhr des bei der Reaktion verbrauchten Sauerstoffs haben. Die Erhöhung der Sauerstoffkonzentration unmittelbar an der Oberfläche der Kohle durch den schnellen Austausch der Luft beschleunigt die Reaktion. Gucken wir uns das im Detail an:

Einfluss der Konzentration: Anschaulich ...

In der linken Hälfte der Abbildung befinden sich halb so viele schwarze Teilchen wie in der rechten Hälfte. Angenommen, ein rotes Teilchen reagiert mit einem Schwarzen, so ist die Wahrscheinlichkeit, dass das eine rote Teilchen auf ein beliebiges schwarzes Teilchen trifft in der rechten Hälfte doppelt so hoch, wie in der linken, da rechts im gleichen Volumen doppelt so viele schwarze Teilchen sind. Rechts ist die Konzentration eines Eduktes gegenüber links verdoppelt. Dadurch ist die Wahrscheinlichkeit für eine Reaktion ebenfalls verdoppelt, wodurch sich auch die Reaktionsgeschwindigkeit verdoppelt.

Würde man entsprechend die Zahl der roten Teilchen vergrößern, hätte das natürlich den gleichen Effekt. Wenn man beide Konzentration verdoppelt, hätte man eine Verdoppelung der Verdoppelung usw..

Die Reaktionsgeschwindigkeit ist proportional zur Konzentration jedes der Edukte. (v ∼ c)

... und mathematisch

Aus "proportional" wird "gleich" durch eine Proportionalitätskonstante k. Betrachten wir eine einfache Reaktion, bei der ein Teilchen A zu einem Teilchen B reagiert, so ergibt sich damit:

A → B
v ∼ c(A) bzw. v = k · c(A)

Die Konstante k wird Geschwindigkeitskonstante genannt und weiter unten noch genauer betrachtet.

Für die Reaktion A + B → C gilt analog:

v = k · c(A) · c(B)

Auf den ersten Blick ist die Reaktion zweier gleicher Teilchen miteinander etwas eigenartig.... Nehmen wir die Bildung eines Sauerstoffmoleküls aus zwei Atomen als Beispiel:

2 O → O₂

Wie soll nun die "2" von "2 O" berücksichtigt werden? Im Grunde ist es ganz einfach. Anstelle von "2 O" ließe sich auch "O + O" schreiben und damit wären sowohl A als auch B aus dem vorherigen Beispiel Sauerstoffatome und es ergibt sich:

v = k · c(O) · c(O) = k · (c(O))²= k · c²(O)

Für die allgemeine Reaktion von oben ergibt sich dann folgendes als allgemeine Gesetzmäßigkeit:

a · A + b · B → d · D + e · E
v = k · c^a(A) · c^b(B)

Reaktionsordnung

Wie oben zu sehen, beeinflusst die Zahl der an der Reaktion beteiligten Teilchen die Reaktion sehr stark, weshalb man die Reaktionen nach der Anzahl der beteiligten Teilchen unterscheidet.

Reaktionen erster Ordnung sind solche, die nur von der Konzentration einer einzigen Komponente abhängen, also z.B: Zerfallsreaktionen. Entsprechend ist die Auftretenswahrscheinlichkeit und damit auch die Reaktionsgeschwindigkeit sehr hoch. Solche Reaktionen erster Ordnung folgen einem Geschwindigkeitsgesetz erster Ordnung wie folgt:

Reaktion 1. Ordnung: v = k · c(A)

Bei Reaktionen deren Geschwindigkeit von der Konzentration zweier Komponenten oder quadratisch von der einer Komponente abhängen spricht man von Reaktionen zweiter Ordnung.

Reaktion 2. Ordnung: v = k · c²(A) oder v = k · c(A) · c(B)

In der gleichen Weise könnte man nun Reaktionen der x-ten Ordnung betrachten. Allerdings sind Reaktionen höherer Ordnung als 3 extrem selten und normalerweise nur scheinbar "eine" Reaktion. I.d.R. sind solche Reaktionen tatsächlich mehrere aufeinanderfolgende Reaktionen niedrigerer Ordnung - für die mathematische Behandlung ist das aber oft egal.

Beeinflussung durch Druckänderung

Eine Druckänderung hat nur dann einen Effekt, wenn das System in dem die Reaktion stattfindet durch den Druck in irgendeiner Weise beeinflusst wird. Da Feststoffe und Flüssigkeiten näherungsweise nicht komprimierbar sind, führt eine Veränderung des äußeren Drucks bei ihnen nahezu nicht zu einer inneren Veränderung, Der Druck hat auf chemische Reaktionen nur dann Einfluss, wenn an der Reaktion Gase beteiligt sind. Nehmen wir an, dass sich die beteiligten Gase näherungsweise "ideal" verhalten, dann gilt für sie das ideale Gasgesetz:

p · V = n · R · T
p: Druck in Pa
V: Volumen in m³
n: Teilchenzahl in mol
R = 8,314 J/(mol K) Allgemeine Gaskonstante
T: Temperatur in K

Stellt man diese Formel so um, dass auf einer Seite n/V steht, also Teilchenzahl durch Volumen bzw. die Konzentration, so ergibt sich:

p/(R·T) = n/V = c

Wenn näherungsweise das allgemeine Gasgesetz gilt, dann ist eine Druckänderung also proportional zu einer Konzentrationsänderung aller gasförmigen Stoffe und kann mathematisch wie eine solche behandelt werden.

Eine Druckänderung ist bei einer Reaktion zwischen Gasen identisch mit einer Konzentrationsänderung. Bei einer Reaktion ohne Beteiligung von Gasen hat eine Druckänderung keinen Effekt.

Beeinflussung durch Oberflächenänderung

Eine Oberflächenänderung hat nur dann Einfluss auf das reagierende System, wenn die Reaktion an einer Oberfläche bzw. Grenzfläche stattfindet. Das Reaktionsgemisch muss also ein heterogenes Gemisch wie das obige Beispiel mit dem festen Zink in der flüssigen Salzsäure sein. In diesem Fall beeinflusst die Größe der Oberfläche die Reaktion, da zur Reaktion die Protonen die Oberfläche erreichen müssen. Da jedes Proton während der Reaktion einen Teil der Oberfläche "abdeckt", ist die Zahl der gleichzeitig reagierenden Ionen durch die verfügbare Oberfläche begrenzt.

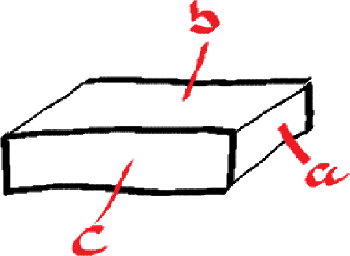
In dem gezeigten Quader gibt es jede der drei Oberflächen a, b und c je zwei mal. An jeder dieser sechs Flächen können die Reaktionen stattfinden. Eine größere Oberfläche würde mehr gleichzeitige Reaktionen ermöglichen. Wenn man nun den Quader in der Mitte teilt, sodass die Flächen b und c jeweils halbiert werden, erhält man zwei Quader und die Gesamtoberfläche hat sich um die beiden Seiten der Schnittfläche vergrößert. Es ist in diesem Beispiel dann zwei mal die Fläche a hinzu gekommen. Je häufiger man den Quader nun teilt, bzw je größer der "Zerteilungsgrad" ist, desto größer wird die Gesamtoberfläche, wobei "je ... desto" hier keine Proportionalität ausdrückt.

Die Reaktionsgeschwindigkeit an Grenzflächen nimmt mit dem Zerteilungsgrad zu.

Beeinflussung durch Änderung der Geschwindigkeitskonstante

Das klingt zunächst mal völlig bescheuert - Änderung einer Konstante. Wenn das möglich ist, ist sie ja nicht konstant und trotzdem heißt sie "Geschwindigkeitskonstante". Tatsächlich ist der Name durch mich nicht änderbar und es ist also egal, ob er mir gefällt. Trotzdem finde ich ihn richtig, denn die Geschwindigkeitskonstante ist tatsächlich so lange konstant, wie man die Temperatur nicht ändert und keinen Katalysator hinzu gibt. Sie ist also immer dann konstant, wenn man eine Reaktion unter konstanten äußeren Bedingungen durchführt.

Im Folgenden wird zunächst anschaulich erklärt, wodurch die Geschwindigkeitskonstante beeinflusst wird. Zum Abschluss machen wir dann, weil doch schöner ist, noch mal etwas Mathematik.

Anschauliche Betrachtung

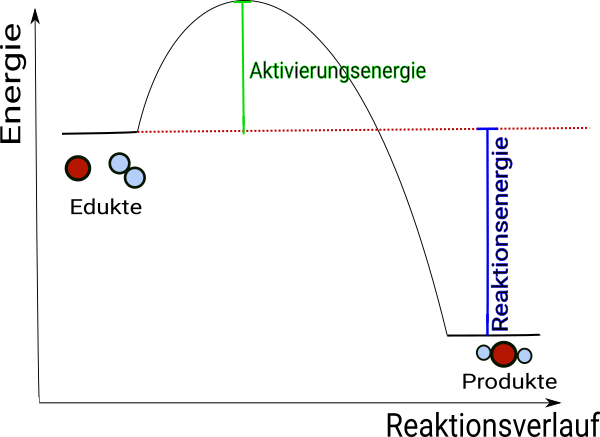
Das beispielhaft dargestellte Energieprofil einer exothermen Reaktion zeigt, was passieren muss, damit die an der Reaktion beteiligten Teilchen miteinander reagieren können.

Das rote Atom und das blaue Molekül müssen beim Zusammenstoß so orientiert sein, dass es zu einer Reaktion kommen kann, bei der das rote Atome zwischen die beiden blauen "rutscht". Das ist nur vom Zufall abhängig und nicht beeinflussbar.

Die Stoßenergie der beteiligten Teilchen muss insgesamt mindestens so groß sein, dass die Aktivierungsenergie aufgebracht werden kann. Die Wahrscheinlichkeit dafür nimmt zu, wenn die mittlere Bewegungsenergie der Teilchen größer wird, d.h. wenn die Temperatur steigt. Bei höherer Temperatur sind alle Teilchen im Durchschnitt schneller und deshalb steht bei einer Kollision mit höherer Wahrscheinlichkeit genug Energie zur Verfügung, um den Aktivierungsberg zu überwinden. Die Reaktion wird also schneller, wenn die Temperatur höher ist und langsamer, wenn die Aktivierungsenergie hoch ist.

Etwas Mathematik

Wenn man davon ausgeht, dass die Aktivierungsenergie für eine Reaktion konstant ist und insbesondere nicht durch Temperaturänderungen beeinflusst wird, erhält man für die Geschwindigkeitskonstante folgende, nach Svante Arrhenius benannte Arrhenius-Gleichung:

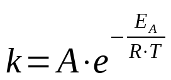
A: Proportionalitätsfaktor mit unterschiedlichen Einheiten je nach Reaktionsordnung
e = 2,71828.....(Eulersche Zahl)
E_A: Aktivierungsenergie in in J/mol
R = 8,314 J /(K · mol) (allgemeine Gaskonstante)
T: Temperatur in K

Der Proportionalitätsfaktor A lässt sich mathematisch aus der Stoßtheorie ableiten und entspricht dem Produkt aus Stoßzahl und Orientierungsfaktor. Dazu spare ich mir hier aber weitere Details und verweise noch mal auf ein gutes Buch zur physikalischen Chemie.

Grenzbetrachtungen

Nehmen wir mal an, die Temperatur würde beliebig klein bzw. groß: Welchen Wert nimmt dann k an?

Lassen wir die Temperatur T gegen unendlich laufen, so wird der Nenner im Bruch des negativen Exponenten immer größer und der Bruch nähert sich somit immer weiter an 0 an. Da "irgendwas hoch 0" immer 1 ergibt, wird der Faktor hinter dem A also bei unendlich hoher Temperatur 1, was bedeutet, dass k = A wäre. Damit käme es also bei jeder Kollision zweier Teilchen in der richtigen Orientierung zu einer Reaktion, was auch der anschaulichen Erwartung für hohe Teilchenenergien entspricht.

Nun ist T = 0 Kelvin ja "verboten", da dann im Nenner des Bruches 0 stünde und Divisionen durch 0 "verboten" sind. Lassen wir also T gegen 0 gehen ohne dass es 0 würde. Der Nenner wird mit kleinerem T immer kleiner und der Zahlenwert des Bruches dadurch immer größer. Da der Bruch ein negatives Vorzeichen besitzt, wird der Exponent mit sinkender Temperatur also eine immer negativere Zahl. Wenn T gegen 0 Kelvin geht, geht der Exponent also gegen minus unendlich und der zweite Faktor hinter dem "A" geht damit gegen 0. Mit sinkender Temperatur wird k also immer kleiner und nähert sich an 0 an. Auch das entspricht der anschaulichen Erwartung, denn mit sinkender Temperatur sollte es immer seltener genug Energie geben, um die Aktivierungsberg zu überwinden.

Zwischen den Grenzen

Insbesondere in der Biologie trifft man häufig auf die sogenannte RGT-Regel (Reaktionsgeschwindigkeit-Temperatur-Regel), die besagt, dass eine Erhöhung der Temperatur um 10 Kelvin die Reaktionsgeschwindigkeit verdoppelt bis verdreifacht. Wenn man sich den Verlauf der k(T)-Funktion für biologisch relevante Reaktionen ansieht, stimmt das auch einigermaßen. Trotzdem ist diese Regel aber eher nur zufällig richtig, denn....

• ... bei biologisch relevanten Reaktionen liegt die Aktivierungsenergie in einem Bereich, den die an der Reaktion beteiligten Teilchen bei Raumtemperatur so einigermaßen überwinden können und...
• ... biologisch relevante Reaktionen werden i.d.R. bei Temperaturen in der Gegend um die Raumtemperatur betrachtet.

Diese Regel wird natürlich total falsch, wenn wir den relativ steilen, mittleren Bereich der Exponentialfunktion für k(T) verlassen und in die Randbereiche der Annäherung an 0 bzw. 1 für den zweiten Faktor gelangen. Tatsächlich ist die RGT-Regel eine grobe Faustregel für qualitative Abschätzungen in der Biologie. Für alle anderen Anwendungen würde ich dringend zum Rechnen mit der Arrhenius-Gleichung raten.